Introduction
What are Panel Methods?
Panel methods (also known as boundary element methods) are numerical schemes for solving partial differential equations (PDE), such as Laplace’s equation for incompressible flows or the full potential equation for transonic flows. The fundamental idea behind panel methods is to divide the aircraft surface into a collection of small, flat surfaces called panels. Each panel is then assigned a distribution of sources, doublets, or vortices, which are mathematical representations of simple flow patterns. These flow patterns are fundamental solutions to the governing PDE, ensuring that the overall flow field satisfies the governing equation.
The general process of a panel method can be broken down as follows:
-
Discretisation: The aircraft surface is divided into a network of panels.
-
Singularity Distributions: Each panel is assigned a distribution of sources, doublets, or vortices with unknown strengths.
-
Influence Coefficients: Mathematical expressions are derived to calculate how the flow from each panel influences the flow at every other panel.
-
Boundary Conditions: Boundary conditions are imposed at specific points on the panels to ensure the flow adheres to the desired physical behaviour, such as no flow penetrating the aircraft surface.
-
Solving the System: The influence coefficients and boundary conditions form a system of equations that are solved to determine the strengths of the source, doublet, and/or vortex strength on each panel.
-
Flow Field Calculation: Once the singularity strengths are known, the flow velocity and pressure can be calculated at any point in the flow field.
-
Force and Moment Calculation: By integrating the pressure distribution over the aircraft surface, the overall aerodynamic forces and moments can be determined.
Because they deal only with surface-based meshes and unknowns, panel methods are highly efficient for analyzing complex aircraft configurations, especially compared to more computationally intensive methods like Navier-Stokes solvers. They find wide use in the aerospace industry for preliminary design studies, evaluating aerodynamic loads, and understanding flow behaviour around intricate geometries.
Why FlightStream?
FlightStream is a modernized panel-method based aerodynamic solver. The original inviscid theory is enhanced with several novel features to provide a more realistic and comprehensive aerodynamic analysis tool compared to legacy panel codes. These enhancements include (but are not limited to):
-
Compressibility Models: FlightStream goes beyond incompressible flow analysis by including compressible flow models, enhancing its capability to simulate a wide range of flight conditions up through hypersonic flow.
-
Integral Boundary Layer: FlightStream includes an integral boundary layer model that accounts for the effects of viscosity on the flow. This allows for more accurate predictions of aerodynamic loads, especially at high angles of attack.
-
Viscous-Coupling Equations: While traditional panel codes primarily focus on inviscid flow, FlightStream incorporates viscous-coupling equations to better model the thickening and decambering effects of boundary layers.
-
Advanced Boundary Conditions: Unlike earlier panel codes, FlightStream introduces advanced boundary conditions, including actuator discs for simulating propellers and jet exhausts.
-
Unsteady Flow Solver: FlightStream has an unsteady flow solver that can be used to simulate the aerodynamics of complex, time-varying maneuvers.
-
Time-Accurate Capabilities: FlightStream boasts time-accurate simulation capabilities, enabling analysis of dynamic scenarios such as trajectory simulations and rotor motions, a feature lacking in many legacy panel codes.
-
Relaxed Vortex-Wake Filament Method: Unlike simpler wake models, FlightStream uses a relaxed vortex-wake filament method to realistically simulate complex and unsteady wake dynamics. This allows for more accurate representation of wake interaction with downstream components.
-
Efficient Algorithms: FlightStream leverages computationally efficient algorithms, such as agglomerate multipole and recursive, octree-based calculations to reduce computational time.
-
Modern GUI: More than just a solver, FlightStream is accessed through a user-friendly graphical user interface (GUI) with full support for CAD integration, meshing, post-processing, and visualization.
-
Scripting API: Large batch runs can be automated using the FlightStream scripting API. Users can generate aerodynamic databases and conduct massive design space exploration quickly and autonomously.
The combination of these features makes FlightStream a powerful tool for modern vehicle design and analysis while ensuring ease of use, high accuracy, and computational efficiency.
Fundamental Flow Equations
For Newtonian fluid the fundamental flow equations are given be the continuity equation:
and the momentum equation, also known as the Navier-Stokes equation.
For inviscid flow, the Navier-Stokes equation reduces to:
Through some manipulation it can be shown the inviscid momentum equation can take the following form.
If we assume irrotational flow and introduct the velocity potential $u_{i}=\frac{\partial \phi}{\partial x_i}$ we can rewrite the above equation as:
And finally applying the incompressible assumption to the continuity equation we get the following:
Subsonic Solver
The potential flow equation is used to define an inviscid, irrotational, and incompressible, and flow. The potential flow Laplace equation defines the smooth behavior of the flow field:
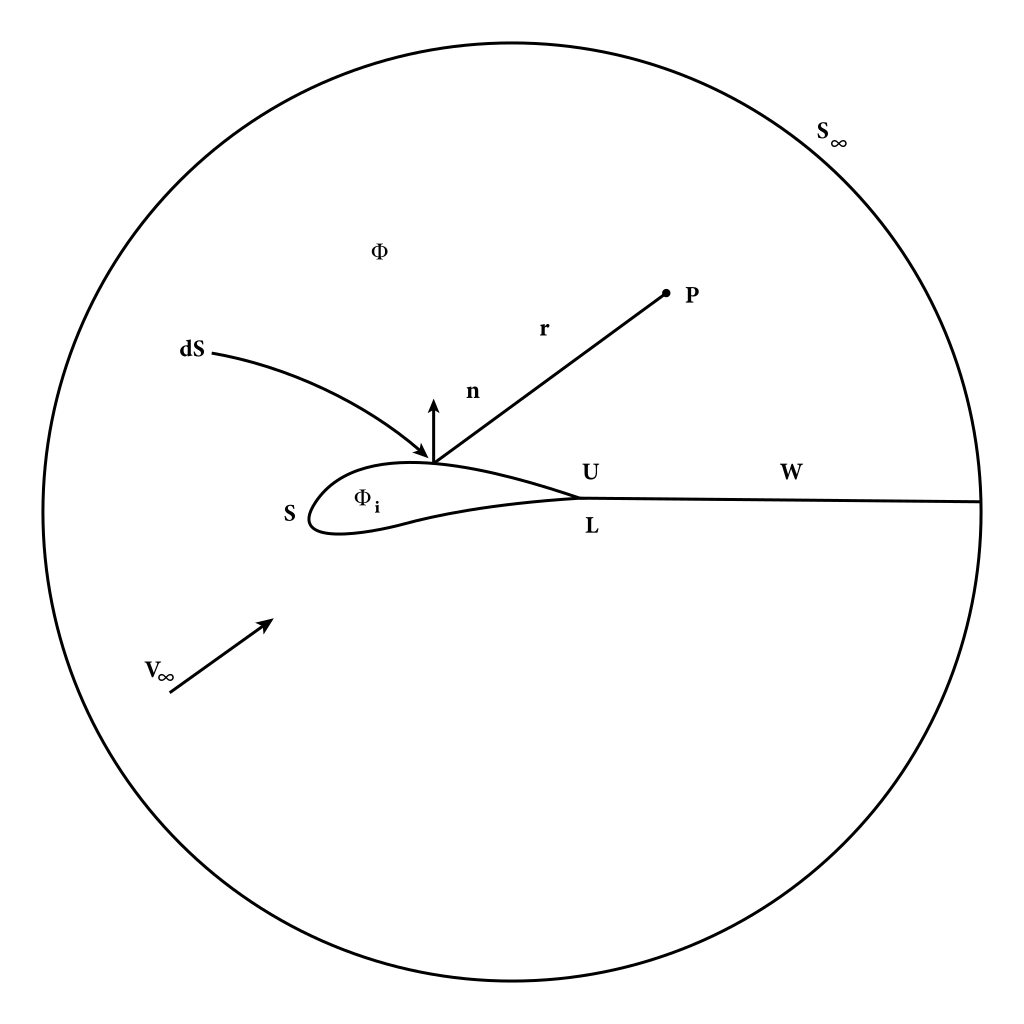
For a body, , immersed in a potential flow field the velocity, Green’s theorem can be applied to the inner and outer surfaces to obtain the following relation:
Where the doublet and source primitives are defined as, and , respectively. Thus, the potential at any point in the flow field may be determined as the sum of source and doublet influences integrated across each panel. The gradient of this may also be taken to find the velocity induced at any point in the flow field.
In addition to approximating the surface by a discrete set of panels, the source and doublet strengths are assumed to follow some analytic distribution over each panel (i.e. constant, linearly-varying, etc.). Most often, panel methods incorporate a linear distribution of doublet strength and a constant distribution of source strength across each panel, or quadratic and linear distributions of source and doublet strength, respectively. This is because the source strength represents a jump in velocity across a panel, while the gradient of doublet strength represents a jump in velocity. Some panel methods instead use constant distributions for both sources and doublets; however, this is typically only done for subsonic methods. For a given body and freestream condition, the values of and on each panel are not known a priori. These distributions may be written in terms of some finite set of unknown source and doublet parameters. By enforcing as many boundary conditions as there are unknown source and doublet parameters, a linear system of equations may be formed. This system of equations will be linear because the induced potentials and velocities are linear in the source and doublet strengths. Then, by solving this system of equations, the unknown source and doublet parameters may be determined. Once these are known, the flow properties at any point on the body or in the flow field are easily obtained.
Boundary conditions can be enforced by assuming that the nature of the flow is known at certain locations called control points. With a boundary condition vector the nodal doublet strengths can be found by
where is the boundary condition vector and is the aerodynamic coefficient matrix.
FlightStream uses a Neumann boundary condition to enforce the boundary conditions. A Neumann formulation specifies the derivative at the boundary of the system. In the context of panel methods this is the derivative of the velocity potential at the boundary. Recall that the derivative of a velocity potential is a velocity; therefore, the Neumann formulations of panel methods are velocity-based formulations and the [AIC] matrix is populated with velocity influences [1].
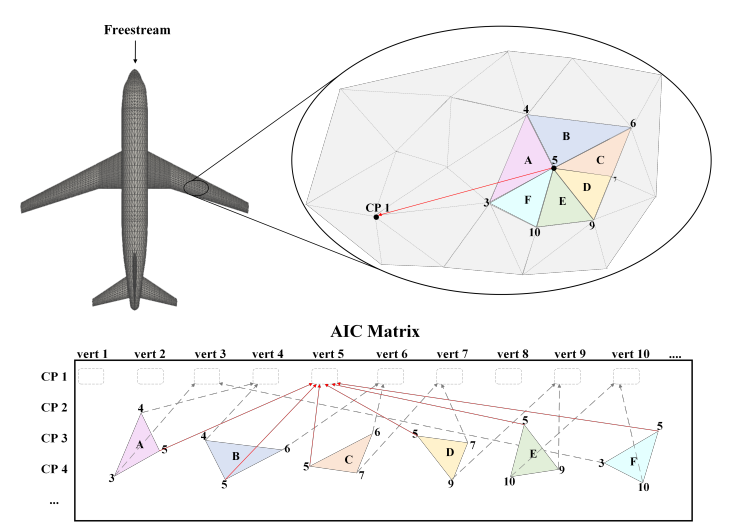
The boundary conditions are enforced at control points that are placed throughout the mesh at the center of panel face. Once placed, there is a geometric relationship between a control point and the mesh vertices and panels. A set of aerodynamic influence coefficients can be calculated for a control point. These influence coefficients are based on the relative position, orientation, and singularity distributions of the panels. Rather than setting a doublet distribution for each panel and measuring the flow at the control points, panel methods define the flow at the control points (ideally representing physical flow conditions), and then solve for the required doublet strength distributions of the panels [1].
The rows of the [AIC] matrix are associated with control points and the columns are associated with mesh vertices. Each row contains coefficients representing the influence of each vertex on that row’s control point. The elements of the [AIC] matrix are populated as shown below.
Surface Blowing
A solution to the above requires that the Neumann boundary condition be satisfied on the surface:
Where is the normal velocity on the boundary which is 0 in the absence of transpiration (later it will be shown that a non-zero transpiration velocity allows for the capture of some viscous effects on the surface). is the local velocity on the boundary and may be composed of several parts due to body rotation (indeed this is how rotational flow fields are modeled in FlightStream). In the simplest steady case the above equation reduces to:
Given a displacement thickness, , the boundary condition becomes:
where the first term represents the rate of growth of the boundary layer, and the second term, , is positive for outflow and negative for inflow. The boundary layer term is typically zero at the start of the calculation and is then updated during each viscous/potential iteration cycle, as described in Section Viscous Modeling.
Wake Treatment
FlightStream employs a cutting-edge relaxed vortex-wake filament method to capture the effects of the wake. At each trailing edge of the body, a wake filament is released. This has the capability to resolve around solid bodies automatically and has inbuilt vortex stretching and disintegration models. The latter enables the modeling of full volumetric effects and to study the interactions between various components while maintaining solution run times measured in minutes. Traditional free wake panel methods have issues with singularities when wakes intersect solid bodies.
The unstructured surface mesh drives the wake to also be unstructured since the trailing edges (TE) are not directionally mapped. In FlightStreams, the concept of “wake strands” (as opposed to wake sheets) emenating from mapped vertices determine the wake geometry.
Once the trailing edges are marked, the vertex pool corresponding to these edges is available from the global vertex map. These vertices become the starting point, or nodes, for the individual wake strands. Since no additional vorticity sources or sinks are added by the wake, the net vorticity of the geometry remains conserved and the wake propagates only the required vorticity to satisfy the Kutta condition at the trailing edges.
Vorticity strength reductions downstream of the trailing edge can only occur due to viscous effects. This is modeled using the application of the Lamb–Oseen vortex model obtained from the exact solution of the Navier–Stokes equations for a laminar 2D vortex. Knowing the initial vorticity shed into the strand at the trailing-edge node, the Lamb–Oseen model provides the vorticity decay equation as:
In the above equation, the time used corresponds to the solver pseudotime and starts at zero at the trailing edge. It is marched alongside the strand (using values of local velocity and the discretization size of the relaxed wake, which is fixed to the average mesh edge length) until the termination of the wake downstream at the Trefftz plane. All strands are projected or terminated upon intersection with the Trefftz plane.
Integrated Circulation
The method of integrated circulation works by evaluating the vorticity along a series of two-dimensional cross sections encompassing the entire geometry. These cross sections can be aligned with their planar vectors directed orthogonally to the freestream and load vectors. The arbitrary distribution of vorticity on the unstructured surface mesh can therefore be converted into directional vorticity along the required load vectors. An example of such cross sections is shown in Figure 4.
The vorticity for each of the cross sections is evaluated by the application of the generalized circulation equation along the perimeter of the cross section. This is easily done once the vorticity on the surface mesh has been evaluated in the solver. Since we can evaluate the velocity induced by a vortex ring at any point in space around the body using Eq.[eq:vortex_ring_velocity]), we discretize the cross section along its rectangular perimeter (Fig.[fig:cross_section_discretization]). We then evaluate the induced velocity from all of the surface vortex rings on each of the discretized vertices of the cross sections. Once a distribution of velocity along the vertices of the cross section is known, the net, integrated circulation of that cross section is evaluated using the numerical formulation of Stokes' theorem:
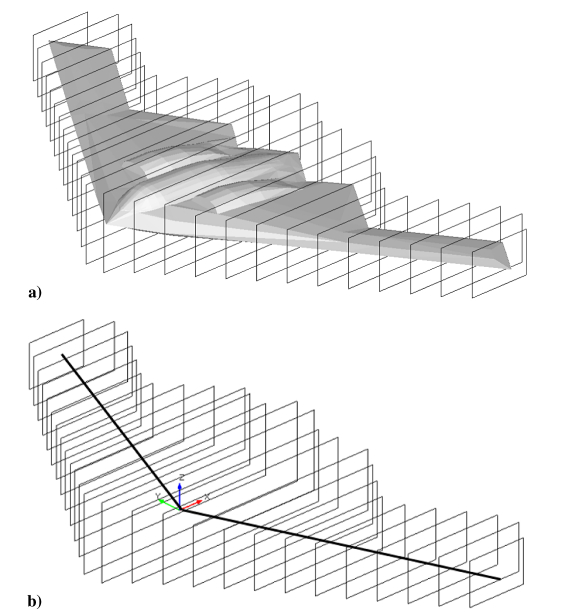
Treated in isolation in two-dimensional space, defined by the plane of the arbitrary cross section, the aerodynamic loads from this integrated circulation could be evaluated from the Kutta–Joukowski theorem [2]. A series of these cross sections enclosing the arbitrary three-dimensional body Cross sections a) allows us to convert an unstructured distribution of bound surface vorticity into adjacent sections of two-dimensional net circulations, thereby reducing them to the Prandtl lifting-line theory Cross sections b), with all the inherent benefits in load computations as provided by this formulation.
If the cross-section planes are aligned orthogonally to the freestream and lift vectors, then their alignment is identical to a lifting-line distribution of integrated vorticity along a rectangular wing. Consequently, the integrated vorticity of each cross section is identical to the "bound" vorticity from the Prandtl theory. The downwash between each of these cross sections is then evaluated by treating each cross-section bound vorticity as shedding a horseshoe-shaped vortex aligned with its planar and freestream vectors.
Furthermore, spanwise loading distributions of arbitrary bodies can also be evaluated through this approach by plotting the loads evaluated for each cross section and plotting them in spatial locations on the abscissas. This entire formulation therefore reduces an arbitrary surface distribution of vorticity to the form of the Prandtl theory, and therefore yields the known formulations of induced lift, drag, and downwash velocities:
For the sake of reading convenience, each of these cross sections will hereafter be referred to as an integrated circulation loop (ICL). In numerical application, the ICLs are discretized using the average edge size of the underlying surface mesh. The spacing between ICLs is also discretized using the same reference values. It is possible to include other discretization values, and this can have a varying effect on the solution fidelity, depending on the complexity of the geometry in question.
Subsonic Solver
In the Subsonic solver, the compressibility correction is applied via the standard Prandtl-Glauert rule. This is done by scaling the freestream velocity and density by the factor , where is the Mach number. This correction is applied to the freestream conditions and the body, and is used to correct the flow field and forces/moments. Typically this correction is only valid up to a Mach number of about 0.6. The user can easily enable the Incompressible solver to bypass this correction. If a higher fidelity compressibility analysis is required, then the user may use on of the several available transonic/low-order supersonic/high-order supersonic/hypersonic methods.
Surface Pressure Coefficient Calculation
After solving for vertex doublet strengths, the velocity and pressure can be solved for at any point on or off the body. The surface velocity, , is given by:
where is the freestream velocity magnitude and is the freestream direction vector. For incompressible flows, the pressure coefficient at a point is given by:
For compressible flows, the isentropic pressure coefficient at a point is given by:
Where is the freestream Mach number and is the ratio for specific heats (default value is 1.4). With surface pressures, force coefficients in the , , and directions are found with the summation
where is the body reference area (such as wing area), is the pressure coefficient at a panel centroid, is the panel area, and is the panel normal vector.
Boundary Conditions
In FlightStream, the boundary conditions are critical for the accurate simulation of aerodynamic flows. The following sections provide an overview of the boundary conditions implemented in FlightStream.
Trailing Edges
The trailing edge boundary condition is crucial for the accurate simulation of aerodynamic flows in panel methods, such as FlightStream. Trailing edge boundaries are essential for satisfying the Kutta condition, a fundamental principle in aerodynamics dictating that the flow must leave the trailing edge of an airfoil smoothly. Failure to meet this condition leads to unrealistic pressure distributions and inaccurate lift predictions. In FlightStream, trailing edge boundaries are marked as special edges on the surface mesh, where wake vortex filaments originate. The strength of these filaments, representing the shed vorticity, is determined by the difference in flow velocity above and below the wake.
FlightStream offers two types of trailing edge boundaries: Standard-Kutta and Relaxed-Kutta. In the Standard-Kutta type, the net circulation at the trailing edge is fully shed into the wake. Conversely, in the Relaxed-Kutta type, only half of the net circulation is shed, suitable for situations where the geometry of the trailing edge is not sharp, such as a rounded fuselage. The accurate placement of trailing edges is paramount for the correctness of the simulation. FlightStream provides several ways to mark trailing edge boundaries, including automatic detection, manual selection, defining perimeters around base regions, and importing from external files.
Wake Termination Nodes
Wake termination nodes are used in conjunction with trailing edges to control the behaviour of the wake vortex filaments. These nodes mark locations where the wake filament should be clipped, preventing the formation of unrealistic tip vortices in specific situations, such as at the junction of a wing and fuselage.
Base Pressure Region
Base pressure regions are used to model the surface-pressure effects of regions of bulk separated flow. In FlightStream®, these regions are explicitly defined by the user. A uniform is applied for the base region during solve time. This value can be user-defined or an empirical model can be used.
FlightStream implements a novel method to calculate the base pressure as a function of freestream Mach number. This model is based on a regression of various experimental data. The base pressure coefficient monotonically increases with decreasing Mach number in the subsonic regime and with increasing Mach number in the supersonic regime. Outside the transonic regime, there is relatively little variation in the base pressure coefficient across various configurations. However, in the transonic regime the base pressure coefficient appears to be a function of more than the freestream Mach number, Base pressure model implemented in FlightStream shows the data is not collapsing for these Mach numbers. For supersonic flows, the base pressure coefficient is bounded from below by the vacuum pressure coefficient (solid black line in the figure).
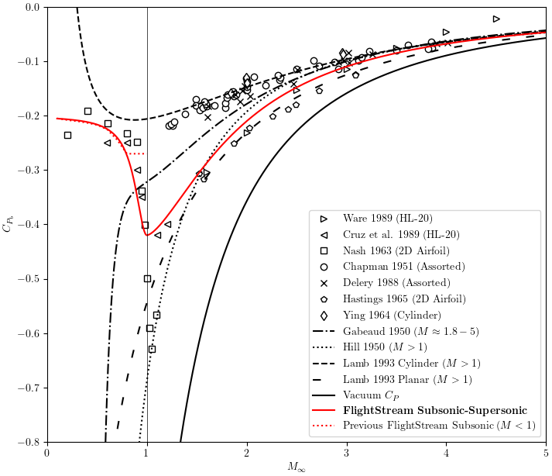
To give an approximate fit to the data shown, the following base pressure model is proposed. For subsonic freestream Mach numbers, the pressure coefficient is given by 1.
For supersonic freestream Mach numbers, the pressure coefficient is given by 2.
These equations both predict a base pressure coefficient of -0.42 at . This model is shown in Base pressure model implemented in FlightStream as the solid red line. Note that this supersonic model can predict pressure coefficients lower than the vacuum pressure for high freestream Mach numbers. Thus, in practice, the supersonic base pressure coefficient is the greater between the vacuum pressure coefficient and that predicted by 2.
While this model yields reasonable results the user is encouraged to run experiments or consult literature for values for their specific application.
Turbulent Trip Edges
In many situations, boundary layer transition is deliberately induced. On production vehicles, imperfections or intentional surface features can act as trip points. In wind tunnel tests, researchers often use physical trip strips to force transition at a desired location, ensuring consistent flow behaviour for measurements. Turbulent trip edges in FlightStream are a boundary condition used to trigger artificial boundary layer transition from laminar to turbulent flow. This is important because, in real-world scenarios and wind tunnel testing, various factors can induce early transition, impacting the overall flow behaviour and aerodynamic characteristics. Once trip edges are defined, FlightStream’s viscous solver incorporates them into the boundary layer calculations. The primary impact is the shift in boundary layer characteristics, influencing parameters like skin friction, displacement thickness, and momentum thickness, ultimately affecting the predicted lift, drag, and moment values.
Actuator Discs
Actuator disc models are instrumental in representing steady-state effects of inherently unsteady systems like propellers in aerodynamics. These models simulate the impact of momentum additions in flow fields due to propulsion components, offering insights into how devices like propellers influence surrounding airflow. The theory behind actuator discs provides an efficient way to estimate the aerodynamic effects of propulsion systems.
Types of Actuator Discs Actuator discs generally simulate the primary propulsion effect of propellers:
-
Propeller Actuator Disc (Conway Model): This model represents the effects of a propeller operating under steady-state conditions, often used in cruise-condition simulations to study how propellers modify the overall flow field.
Each actuator disc applies specific boundary conditions and momentum additions to reflect the characteristics of the propulsion system.
Actuator discs possess several modifiable physical parameters:
-
Dimensions and Orientation: The radius or elliptical dimensions of the actuator disc can be adjusted, allowing for alignment with the intended propulsion component’s geometry.
-
Velocity Distributions: Actuator discs enable custom-defined velocity distributions across their surfaces. For instance, propeller discs may include swirl velocity to account for rotational flow effects in the slipstream.
-
Custom Thrust Profiles: Propeller discs can integrate custom thrust profiles, offering a more accurate representation of the non-uniform slipstream velocities, especially important for advanced or distributed electric propulsion systems.
Although actuator disc models generally offer steady-state approximations, unsteady simulations can provide deeper insights in dynamic scenarios, such as varying propeller pitch or RPM. In summary, actuator disc models are crucial for simulating propulsion effects on surrounding flow fields, enabling aerodynamic evaluations of various propulsion systems in aircraft design. Understanding the principles and parameters associated with these models allows for precise and adaptable simulation setups tailored to different aerodynamic and propulsion studies.
Thrust Distribution Examples
The following examples show the thrust distributions for various propeller blade shapes. The presented equations can be used to create a thrust profile and then applied to a Custom actuator disc in FlightStream.
Generic Thrust Distribution
Let the thrust distribution over a single blade of a propeller be given by:
where is the non-dimensional blade location (varying from 0 to 1), is the non-dimensional location of the hub, and is a scaling coefficient. This is shown in Thrust distribution for a generic propeller blade.
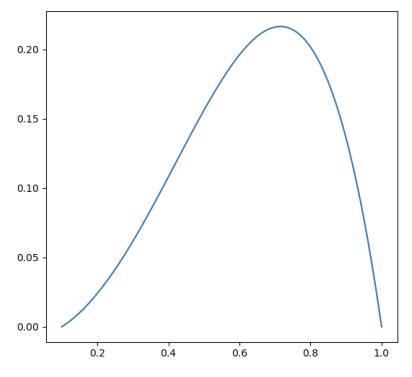
This can be rearranged into the form:
where:
If the total thrust, , produced by the propeller is known, then may be determined from:
where is the number of blades and is the tip radius (dimensional). and may be either dimensional or non-dimensional coefficients, so long as they are consistent with each other.
Elliptic Thrust Distribution
The thrust distribution over a single blade of a propeller may also be given by:
where is a scaling constant and is the non-dimensional blade location. We call this the elliptic distribution.
Again, may be determined from:
Note that for this distribution, we assume no hub. If we let:
then:
Thus:
Viscous Modeling
Given the inviscid solution, FlightStream® estimates the boundary layer properties such as thickness, , momentum thickness, , and shape factor for both laminar and turbulent flows. Additionally, the viscous effects can be used to virtually perturb the boundaries and modify the inviscid bulk flow.
Laminar / Turbulent Boundary Layer
Two models for the boundary layer are implemented in FlightStream®: laminar and turbulent. A boundary layer transition model is also implemented. All of these models are two-dimensional methods implemented along the on-body surface streamlines. These integral methods are computationally efficient and can be applied to any general three-dimensional wall boundary with exceptions of regions involving three-dimensional cross flow. The laminar boundary layer analysis method used in FlightStream® is the standard two-parameter model of Thwaites [3] integral method with the momentum integral equation written as follows:
An integral boundary layer model for compressible turbulent flows has been implemented into the inviscid flow solver. The Standen model is used based on the model’s robustness and versatility for the range of subsonic Mach numbers of interest. The final turbulent boundary layer model implemented has numerical improvements and optimizations over that of the original model developed by Standen , but philosophically follows his work quite closely, with the application to subsonic, turbulent, compressible flows along on-body streamlines. The method is essentially two-dimensional (similar to the laminar model described previously), but is implemented in a quasi-three-dimensional manner inside FlightStream® by assuming that the three-dimensional cross flow terms are not dominant. For the fluid properties outside the boundary layer, the flow is assumed to be isentropic and subsonic, but compressible. The primary differential equations are developed for the turbulent compressible momentum thickness (), and the compressible shape factor (), as described here:
The auxiliary equations needed to complete the above equations are :
Solving these equations numerically (using 4th order Runge-Kutta methods) along the on-body streamline generates all relevant turbulent boundary layer data. This data is then used to compute the boundary layer thicknesses. The skin friction equation used is:
In order to account for surface roughness a modification from Olsen is applied to the surface roughness. In his work, from experiments on rough pipes, it is shown that the overlap layer in the turbulent velocity profile maintains a logarithmic shape and that the intercept at zero velocity is shifted towards higher roughness height. This shift depends on the size of the roughness. For sufficiently large roughness heights, the shift can be shown to have a logarithmic relation with roughness height. As the outer part of the velocity profile is unaffected by the roughness, Coles law of the wake is still applicable for flow over rough surfaces. By including the shift in the intercept in Coles law of the wake as a function of roughness height, it is possible to derive the following expression for the skin friction coefficient () for rough surfaces in the same manner as for the smooth case:
In this equation, is the Reynolds number based on the local momentum thickness of the boundary layer (), is the Reynolds number based on the surface roughness height () and is the local shape factor of the boundary layer.
Boundary Layer Transition
The presence of both laminar and turbulent separation models in FlightStream® allow for the possibility to model complex transitional separation physics along a given surface streamline. A suitable transition model is required to determine the location where a switch between the laminar and turbulent separation models can be performed. The transition model created by Dvorak et.al. is applied in FlightStream®, based on the criteria of robustness and general applicability. The general outline of this model is detailed in this section.
As the local Reynolds number based on momentum thickness gets larger, the laminar boundary layer becomes unstable and small disturbances in the boundary layer begin to amplify rather than damp out. The amplification of disturbances eventually leads to transition to a turbulent boundary layer. The local Reynolds number at which the laminar boundary layer becomes unstable can be correlated with the local pressure gradient by means of the following empirical relationships. The local pressure gradient along the laminar boundary layer on the streamline can be defined as:
Here, is the momentum thickness of the laminar boundary layer; is the kinematic viscosity, is the velocity at the outer edge of the boundary layer (potential flow surface velocity in FlightStream®); and is the coordinate along the surface streamline. The pressure gradient parameter is computed as a field variable along the surface streamline for each mesh face location. The work done by Dvorak et.al. has resulted in the following set of empirical equations for for a range of local Reynolds Number based on the momentum thickness ():
If , as computed by the original formulation using the computed boundary layer data is greater than as computed by these empirical equations, then the laminar boundary layer is marked as unstable. In the unstable region, an average pressure gradient parameter can be defined as:
is the coordinate along the surface streamline where the laminar boundary layer becomes unstable. The local Reynolds number at the transition point can be correlated with by means of the following empirical relationships using :
When , as computed computation is greater than as computed by the empirical equations, natural transition is predicted. The transition from laminar to turbulent boundary layer is assumed to take place instantaneously at the transition point. At this point, the solver switches the separation models from laminar to turbulent. The user is provided an option to toggle between completely turbulent separation models (no laminar transition) or a transitional separation model . An additional field variable for the boundary layer transition model has been implemented into the FlightStream® post-processor to visualize these results .
Performance Enhancements
With the addition of advanced viscous models to FlightStream®, additional computational enhancements have been added to the solver to maintain an scalability to the performance of the boundary layer algorithms. To this end, spatial octree algorithms that mimic the existing Fast Multipole Method implementation (for the inviscid solver) have been implemented for the viscous flow near-wall regions. This allows extremely fast near-field sorting of points closest-to, or inside, a viscous flow region. The Viscous Spatial Tree (VST) is created in the global coordinate system of the solver and increases the memory footprint of the FlightStream® solver by <5% for all cases. However, the performance benefits for viscous modules in FlightStream® are substantial with an otherwise algorithm (where is a very large number of surface mesh faces) being reduced to .
Further performance benefits are obtained by specifying proximity-search boxes in the local coordinate system of the mesh faces being checked for viscous flow. These local-frame proximity boxes are computed at the time of solver initialization and are therefore available without performance penalties for all subsequent analysis work. The localized proximity-search boxes are invoked as a subset within the VST. The height of the proximity search box is the displacement thickness of the local viscous boundary layer flow.
Attachment Lines
FlightStream utilizes a robust model for computing attachment lines and critical points on the inviscid surface-velocity field. This is an enabling requirement for robust coupling with the viscous boundary layer models described previously. It should be noted that the inviscid surface streamlines in FlightStream are computed by solving the Ordinary Differential Equations (ODEs) for a three-dimensional streamline, constrained to the vehicle surface. The implementation assumes a linear variation of the surface velocity field across each surface triangle until a triangle edge is reached. A triangle-to-edge-to-triangle data structure is used to move to the adjacent triangle where the integration process is continued. The streamline ODEs are integrated in reverse, starting at a point near the base of the vehicle, and ending at the stagnation point.
Attachment lines can be located using numerical methods based on the vector field topology of such inviscid flows . The topology of a vector field consists of critical points, i.e., points where the velocity is zero, and the tangent curves (instantaneous streamlines) which connect these points. Because the velocity at a critical point is zero, the velocity field in the neighborhood of the critical point is determined by . Critical points are classified, to a first order approximation, by the eigenvalues and eigenvectors of . Common classifications include a saddle, node, spiral, and center.
Using the inviscid surface velocity field generated in FlightStream, the method developed by Kenwright is used to locate the attachment lines. Kenwright developed two automatic feature extraction techniques that locate and distinguish separation and attachment lines on solid bodies in 3D numerical flow fields: (a) Phase Plane Algorithm and (b) Parallel Vector Algorithm.
These algorithms are based on eigenvalue analysis of the velocity gradient tensor and perform a local analysis of the vector field rather than a global analysis of the entire flow field. These methods are useful for analyzing large partitioned data sets, such as those computed on distributed memory architectures, because the elements can be processed in parallel. In 2D flows, this can occur only at critical points (half-saddles) located on 1D boundaries. These critical points are just places where flows along the surface in opposing directions converge and, by continuity, the wall shear stress is zero. In fully 3D flows over a 2D boundary, there are 1D loci where flows in relatively opposing directions meet , but the criterion of zero wall shear stress does not generally hold, because there is almost always flow along the 1D curve. In fact, the wall shear stress can reach zero only at isolated points along these so-called lines of separation.
The key requirement for any implementation of an attachment line method for FlightStream® requires that the technique be local, meaning that an independent test could be applied to each element on the surface of a body. A modified Phase Plane Algorithm [10] was implemented for this effort. This method models the flow over a simple triangular element and identifies flow patterns that contain streamline asymptotes. Given that the velocity vectors are defined at the vertices, a linear vector field [9] can be constructed that passes through the triangle and satisfies the prescribed vectors at the vertices:
Here, is the Cartesian coordinate vector and the tangential velocity or shear stress vector. For a linear vector field, the coefficients and those in the 2x2 (Jacobian) matrix are constants. These constants can be computed analytically by substituting the coordinates and vectors from each vertex into this equation and then solving the resulting set of simultaneous equations. By differentiating this equation with respect to time and then algebraically manipulating the resulting equations, one can produce a pair of second order nonhomogeneous ordinary differential equations. If the determinant of the Jacobian matrix is nonzero, the solution has the form:
Here and are the eigenvalues of the Jacobian matrix and and are the eigenvectors. The two column eigenvectors form the eigenmatrix. The terms and are arbitrary constants that define a particular curve in the phase plane. The constants and are the coordinates of the critical point:
Here, and translate the coordinate system such that the origin coincides with the critical point. A linear vector field constructed in most triangles will have one critical point. However, that critical point will usually lie outside the boundary of the triangle. The critical points that do lie inside triangles correspond to those found by linear vector field topology methods . Using this formulation, tangent curves can be constructed that pass through the triangle. Rather than working in the physical plane of the triangle, we can simplify matters by transforming into canonical coordinates , that is, a coordinate system where the eigenvector directions are orthogonal:
These equations describe all necessary equations for this method. However, a condition under which a streamline asymptote will pass through the triangle is still required, as well as to determine the points of intersection. Tangent curves of the vector field can be constructed in the plane using the above method. This is often referred to as the Poincare phase plane . By eliminating the integration variable, , one can express the trajectories of these curves in terms of an implicit scalar function. For the case where both eigenvalues are real numbers, the solution is either:
The contours of are everywhere tangent to the vector field and may be verified using the relationship , where is the image of the vector field in the phase plane. By differentiating Equation-4 with respect to , the necessary transformation can be obtained, which maps the vector field, , into the phase plane. is an exact solution to a rotational 2D linear vector field, which, in general, will not be divergence-free. A nonzero divergence means that mass is not conserved on the surface of the triangle. The fact that this system can lose mass is physically important because this accounts for fluid that leaves the surface as the flow converges on a separation line. The system will gain mass as the flow returns to the surface and diverges from an attachment line.
The phase portrait can assume one of two orientations in the phase plane depending on whether it is an attracting node or a repelling node . Specifically, streamlines asymptotically diverge from the -axis for a repelling node, while they converge on the -axis for an attracting node. A separation or attachment line will pass through a triangle if the triangle straddles the -axis or -axis in the phase plane. The vertices of the triangle are mapped into the phase plane using the central expression in the above formulation.
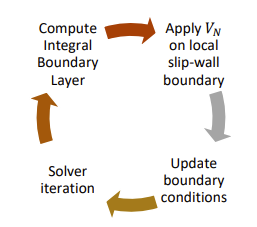
Viscous-Inviscid Coupling
To perform viscous-coupled flow solutions, the laminar and turbulent boundary layer models were integrated with the inviscid solver via displacement of the inviscid boundary equal to the displacement thicknesses of the local boundary layers. A three-dimensional methodology applicable to unstructured surface meshes has been implemented into FlightStream®. The solver coupling takes the following form:
-
Solve the potential flow field over the body and obtain the inviscid surface vorticity distribution.
-
Compute the integral boundary layer
-
Modify the surface flow boundary condition for the potential flow and solve for the second iteration.
-
Repeat steps 1-3 until both the inviscid and viscous flow solutions are converged.
For boundary layers, the displacement thickness indicates the extent to which the surface would have to be displaced in order to be left with the same flow rate of the viscous flow, but with an inviscid velocity profile of . Therefore, the displacement thickness is suited for the measure of displacement needed for the inviscid boundary. Fig. 6 illustrates the philosophical idea for this task.
The second option for inviscid boundary displacement is to simulate the displacement of a fixed surface mesh by blowing a velocity normal to the mesh face. The magnitude of the blowing velocity can be computed by using the momentum flux equations to give:
Here, is the displacement thickness values computed from the previous integral boundary layer computations; is the local streamline velocity outside the boundary layer; and is the direction along the local surface. The transpiration (blowing) velocity is then used to modify the FlightStream® inviscid Neumann boundary condition for the mesh faces using the following equation:
The iterative formulation of the Normal Blowing Boundary approach is illustrated in Fig. 8. The transpiration velocity approach has substantial numerical and practical advantages over the morphing boundary approach in that it does not necessitate morphing the physical mesh (which can cause solver stability and robustness issues, especially in regions involving geometric concavities) or updating the geometry influence matrices, which can be computationally expensive. Based on numerical tests, the transpiration velocity model was chosen as the superior model and implemented in FlightStream®.
Additional reading and validations of these methods in can be found at these references [].
Separation Criteria
In the boundary layer, if pressure in the direction of the flow increases (adverse pressure gradient), the flow can slow down and even reverse. If this adverse pressure is too severe, the boundary layer separates from the surface, leading to increased drag and possibly stall in the case of aircraft wings.
This section discusses the methods used to determine where the flow separates along a surface streamline in FlightStream.
Stratford Separation Criterion (Axial model)
After the inviscid solution is calculated, FlightStream® uses analytical models to estimate where the flow becomes separated. FlightStream® implements a modified Stratfod separation criterion to estimate boundary layer separation location. The Stratford criterion predicts a condition where this separation can be delayed or prevented, even under strong adverse pressure gradients. Stratfod derived an expression for predicting laminar boundary layer separation. [4]
Here is the effective length of the boundary layer and is the origin of the layer. Typically the point of maximum velocity. For turbulent boundary layers, Cebeci-Smith modified Stratford’s original formulation to say that the boundary layer is separated where:
To extend this 1D method to a quasi-3D flow, the pressure gradients are calculated along surface streamlines.
Valarezo Separation Criteria
The Valarezo criteria is a method of determining separation based on the difference in pressure at the leading and trailing edges of a wing. The method uses an empirically-derived "pressure difference rule" to predict maximum lift for complex multielement wing geometries . The pressure difference rule states that at a given Reynolds number and Mach number, there is a specific pressure difference between the suction peak and trailing edge of an airfoil at the maximum lift condition. This rule applies to both single and multielement airfoils. This method tends to predict separation later than Stratford. [5]
Separation Velocity Profile
The Swafford velocity profile is used to determine the velocity profile at the separation point . The full derivation can be found in the reference. The final expression implemented in FlightStream® is:
Where the parameters and are function of and and .
Additionally, FlightStream sets the to zero in separated flow regions.
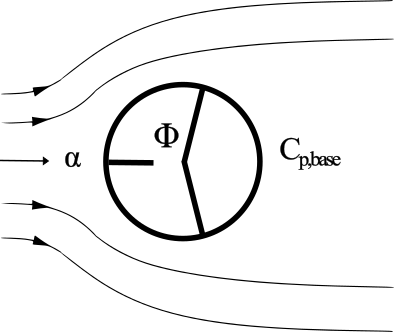
Cylindrical Separation (Crossflow)
In FlightStream®, the CrossFlow (CF) separation model is a method for predicting boundary layer separation from a surface. It assumes that separation occurs at a critical surface inclination relative to the freestream flow. This model approximates the local geometry as an infinite cylinder, identifying panels with a relative flow angle exceeding 90° as being in a separated flow state. For these panels, a uniform pressure coefficient ($C_p$) is applied. The diagram in Figure Figure 5 illustrates the implementation of this approach. This model is typically enabled on fuselage like components. Internal testing has shown the need for enabling this model to capture the fuselage-lift contribution at high angles of attack.
Transonic Solver
The transonic solver in FlightStream is based on a field-panel approach to solving the nonlinear full-potential equation. In a steady motion of an inviscid, isentropic, irrotational flow it can be shown that the nonlinear full potential equation is:
And under the assumption of irrotational, steady, and homentropic flow, the total enthalpy is constant in the entire flowfield.
Mach Number
If the magnitude of is equal to the local acoustic speed (i.e., ), the flow is said to be sonic. The sonic speed, latexmath:[c_s\), is given by
The sonic speed is the speed at which the local fluid speed and the speed of sound are the same. If the flow speed is greater or less than the sonic speed, the flow is called supersonic or subsonic, respectively. From Eqs. 13 and 14, in the case of subsonic flow and in the case of supersonic flow. Thus, the dimensionless parameter is defined as
at any point on a streamline. This quantity is called the Mach number. Based on the inequalities given above, the Mach number will be greater than, equal to, and less than unity for supersonic, sonic, and subsonic flow, respectively. It should be noted that the value for the local Mach number and, consequently, the designation of the flow, is entirely dependent on the frame of reference chosen.
Local-Inclination Solvers
The local-inclination methods in FlightStream for calculating the pressure coefficient on the surface of a body depend solely upon the local inclination of the surface. The inclination of the surface is given by:
where is the local surface normal vector and is the freestream velocity vector. Surfaces where are categorized as windward surfaces, and surfaces where are categorized as leeward surfaces.
In FlightStream, there are two local-inclination methods: the tangent-cone method (focused on low-mid supersonic analysis of slender configurations) and the modified-Newtonian method (focused on high-supersonic/hypersonic analysis of blunt configurations).
Tangent Cone Method
The Tangent Cone method approximates the pressure coefficient as the pressure coefficient on the surface of a cone in the same flow. The solution for the cone pressure coefficient is carried out by solving the Taylor-Maccoll equations for conical flow given as \cite{anderson2003modern}:
and
This is a first-order ODE, which can be solved numerically. The solution procedure is carried out inversely. First, an arbitrary shock angle is assumed. Then the Taylor-Maccoll equations are solved, marching inwards from the assumed shock angle. The deflection angle ( ) is sought where the radial velocity ( ). This deflection angle then becomes the cone angle for the assumed shock angle. The surface pressure coefficient ( ) on the cone is the known. Oblique shock relations and then isentropic relations give the surface pressure coefficient on the cone.
Solving the Taylor-Maccoll equations is computationally expensive. FlightStream does not directly solve these equations for every run. Instead, FlightStream uses a sixth-order polynomial to represent the cone surface pressure coefficient expressed as
through were calculated and tabulated across a range of freestream Mach Numbers and specific heat ratios. When FlightStream is run with the Tangent Cone method, the pressure coefficients on a panel with a given inclination are evaluated based on the polynomials at the nearest tabulated Mach numbers and specific heat ratios to the flight conditions. These values are linearly interpolated between to come up with a pressure coefficient for each panel.
Similarly to the wedge, there is a certain cone angle above which the shock is detached and the Taylor-Maccoll equations cannot be used to predict the surface pressure on the cone. This angle arises during the solution process of the Taylor-Maccoll and is stored and tabulated. When a panel inclination is above the cone for given flight conditions, another pressure method must be used.
For 90% of panel inclinations, the percent error for the interpolated pressure coefficient is within 2% of the exact pressure coefficient. For panel inclinations with a large relative error, the pressure coefficient is very low. As a result, these panels with high relative error have little impact on the overall aerothermal results. This level of accuracy is judged to be of an appropriate level of fidelity for the mid-fidelity nature of the FlightStream code.
Modified Newtonian Method
The original Newtonian method, also referred to as the straight Newtonian method, utilizes the following equation for pressure calculations \cite{anderson1989hypersonic}:
where is the pressure coefficient on the surface and is the inclination angle. The pressure coefficient on the surface as calculated by the straight Newtonian method is independent of Mach number. Lester \cite{grantz1994calibration} suggested a modification to the Newtonian method where is scaled by relating to . is the stagnation pressure coefficient at aft of a normal shock wave given by:
This modification adds Mach number dependence to the Newtonian method. The modified Newtonian method can now be stated as:
The Newtonian methods only apply to the windward surface of the body. Leeward surfaces are handled using Prandtl-Meyer expansion theory as described in Leeward Pressure Coefficients Using Prandtl-Meyer Expansion.
Leeward Pressure Coefficients Using Prandtl-Meyer Expansion
The method for calculating the leeward pressure coefficients used in this work is a Prandtl-Meyer Expansion from the freestream Mach number. The Prandtl-Meyer function is given by
For conducting analysis using the Prandtl-Meyer function, the inclination angle is related to the Prandtl-Meyer function by
This expansion is applied through . The max turning angle is given by
Beyond the max turning angle, the flow is considered as separated and the pressure is determined using the base region relations shown later. Solving the Prandtl-Meyer function results in the Mach number at an expansion surface of inclination . The pressure coefficient on the expansion surface is given as
It should be noted that these calculations yield a positive pressure coefficient even at zero impact angle, and the results generally agree well with experimental data for blunt shapes. However, if the surface curvature transitions gradually to zero slope some distance away from the blunt stagnation point, the method tends to overpredict the pressure. This overestimation occurs because flow characteristics near the nose intersect the curved shock system and are reflected back onto the body. When the zero slope is reached close to the nose—such as in the case of a hemisphere or cylinder—this effect does not have sufficient distance to develop.
|
Note
|
Known Current Limitations
|
Supersonic Linear-Doublet Solver
The supersonic linear-doublet solver is under development and limited beta release as of version 25.1 of FlightStream. The aim of the linear-doublet solver is to provide mid-fidelity solutions in the approximate range of . Its strengths include:
-
Resolution of volumetric shocks and component interactions with only a surface solution.
-
Rapid solution times and low hardware footprint.
Governing Equations
The supersonic linear double solver within FlightStream is based on applying the method of Green’s functions to the Prandtl-Glauert equation [6], [7]. The Prandtl-Glauert equation (also known as the linear potential equation) is given by
where is the Mach number of the undisturbed freestream (assumed to be aligned with the x-axis) and is the perturbation velocity potential. The total velocity potential is given by:
where is the velocity potential (i.e. is the fluid velocity), is the magnitude of the freestream velocity, is the freestream potential, and is the perturbation potential. The Prandtl-Glauert equation is derived from the continuity equation, Euler’s equations of motion, and the energy equation by assuming the flow is homentropic and irrotational, and neglecting nonlinear terms [8]. This makes the Prandtl-Glauert equation a reasonably accurate model of fluid flow for small-perturbation flows outside of the transonic and hypersonic regimes [8].
One critical assumption made in deriving the Prandtl-Glauert equation is that devitations from the freestream Mach number are assumed small enough to be neglected. This essentially means that the Mach number is assumed to be constant throughout the flow. This has several important consequences:
-
All characteristic surfaces are right cones aligned with the freestream velocity vector. The half angle of these surfaces is constant and equal to the Mach angle. This means that all shocks and expansion fans are predicted to occur at the same angle, regardless of upstream or downstream flow properties. This is strictly correct in the limit of infinitessimally weak shocks and expansion fans. For weak shocks and expansion fans, this assumption is reasonable, but the validity of this decreases with increasing shock strength.
-
Only flows that are purely subsonic or purely supersonic can be modeled. If the flow changes character locally, then the governing equation needs to switch character (i.e. from elliptic to hyperbolic, or vice-versa) to capture that flow behavior. This does not happen with the Prandtl-Glauert equation, as is constant. If for any simulation the flow is found to change locally from supersonic to subsonic, or vice-versa, the results should be discarded, or at least treated as highly suspect.
Applying the method of Green’s functions, the perturbation velocity potential at any point in the flow may be found from [8]
where is the point of interest, is if the flow is subsonic and if the flow is supersonic, is the Green’s function for the Prandtl-Glauert equation, is the surface of the configuration being analyzed, and are distributions of source and doublet strength across , respectively, and denotes the conormal derivative, described subsequently.
The supersonic Green’s function is given by [7]
where is the integration point on . The region where for a fixed point is called the domain of dependence of point . Alternatively, the region where for a fixed point is called the domain of influence of point . These domains are shown schematically for a single point.
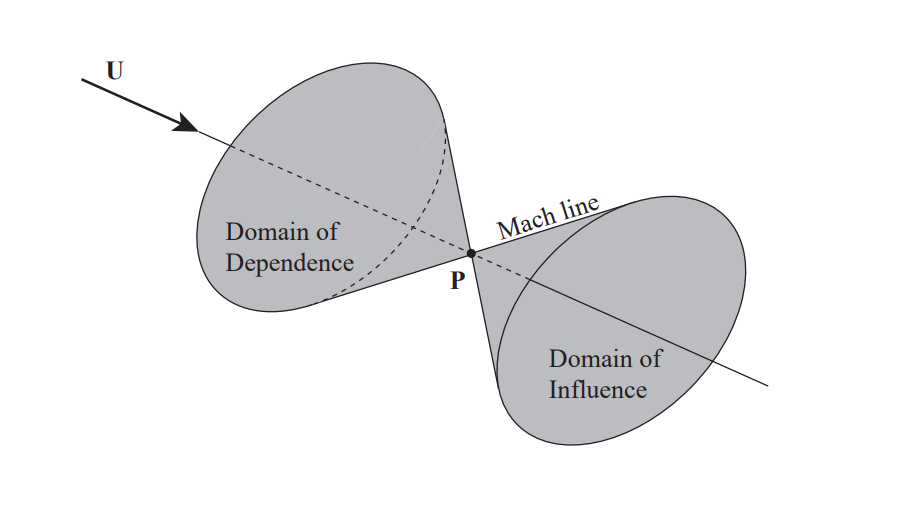
The subsonic Green’s function is identical, except that it is nowhere zero. Thus, in subsonic flow, the domains of dependence and influence for any point are the entire fluid region. This makes sense given that the Prandtl-Glauert equation is elliptic for subsonic flows.
The conormal derivative is given by
In these equations, is the outward normal to , and is called the conormal vector. Green’s function may be solved approximately by breaking into discrete surfaces, called panels. Doing so and allowing for the presence of a discretized wake surface, Eq. 26 becomes [8]
where and are analytic distributions of source and doublet strength across each panel. For a general configuration, and are not known a priori. The method used here for determining and will be discussed later. In Eq. 27, the doublet influence on the velocity potential has the opposite sign from that of the source influence. Because of this, panel methods traditionally define a surface distribution of doublets as inducing flow through the surface in the direction opposite the normal vector (e.g. see [19, 46]). This is different from the standard definition of a doublet where flow is induced in the same direction as the normal vector. For consistency with the literature, the traditional panel method definition is maintained in FlightStream.
Sub- and Superinclined Panels
The nature of linearized flow theory on which FlightStream is based leads to some peculiar practical considerations. The most important of these considerations is the difference between subinclined and superinclined panels.
As discussed above, one basic assumption built into the Prandtl-Gluert equation is that the Mach number is everywhere constant. This then means that there is a constant characteristic angle (the Mach angle) throughout the flow, and all shocks/expansions have that same angle relative to the freestream. In addition, the cone bounding the domain of influence of any given point also has this angle.
Subinclined panels are inclined to the freestream at an angle less than the Mach angle. Superinclined panels have an inclination angle greater than the Mach angle. The implementations of these two types of panels are fundamentally different, and currently, only subinclined panels can be used in FlightStream. Future work will include implementing superinclined panels. However, their use will be limited due to the nature of linearized theory.

Boundary Conditions
In order to understand the boundary conditions used in the supersonic linear doublet solver, it is first important to understand how the surface source and doublet distributions relate to the velocity potential on the outside and inside of the configuration being analyzed. It may be odd to think of there being a velocity potential on the inside of the configuration, but it is there and needs to be taken into account. Source panels result in a jump in the conormal derivative of velocity potential, which is related to linearized mass flux [7]. The magnitude of this jump is equal to the local source strength. Similarly, a doublet panel induces a jump in the value of the velocity potential going from the inside of the panel to the outside. If the doublet strength is not constant, then there is also a jump in local velocity equal to the local gradient of doublet strength.
Knowing these properties of source and doublet panels allows for clever applications of boundary conditions. The standard boundary condition for compressible panel methods is called the Morino formulation. The Morino formulation begins with assuming that the inner perturbation potential is everywhere zero. Using the properties of source panels and applying a condition of zero normal linearized mass flux on the outer surface of the configuration, it can then be derived that
Then, the panel doublet strengths are determined based on the condition that the total internal perturbation potential due to both sources and doublets must equal zero. This Morino formulation has been used in numerous panel methods. It provides very accurate results for small-perturbation flows at low-supersonic Mach numbers.
However, early in the development of the supersonic linear-doublet solver, it was determined that the Morino formulation fails to produce realistic results for high-inclination panels. For example, on delta wings at high angles of attack, the pressure coefficient on leading-edge surfaces was being predicted as negative, resulting in an inverted drag polar and even negative wave drag. It should be remembered that the Morino formulation is derived form a condition of zero normal linearized mass flux. This linearization becomes less valid as the panel inclination increases.
In an attempt to improve accuracy, a velocity-based boundary condition was implemented. This is very similar to the Morino formulation and begins with the assumption of zero inner perturbation potential. However, the condition applied on the outer surface is one of zero normal velocity. Just as with induced potential and linearized mass flux, this outer velocity can be expressed as a linear combination of the surface source and doublet strengths. As with the Morino formulation, the inner perturbation potential is chosen to be zero. But unlike the Morino formulation, the normal velocity on the outside of each panel is a function of both the local source and doublet strengths. Because of this, the source strengths are included as unknowns in the linear system of equations, rather than being calculated a priori.
Through thorough testing, some significant aspects of the velocity-based boundary condition were determined:
-
At low inclination angles, the velocity-based boundary condition produced less-accurate surface pressure results than the Morino formulation.
-
At high inclination angles, the accuracy of the velocity-based boundary condition was better than that of the Morino formulation. In particular, the velocity-based boundary condition never broke down and predicted negative pressure coefficients even at inclination angles approaching the Mach angle.
-
For all inclination angles and Mach numbers, use of the second-order pressure rule (discussed below) resulted in greater accuracy with the velocity-based boundary condition than the isentropic pressure rule did.
The supersonic linear-doublet solver relies on a mix of Dirichlet and Neumann boundary conditions.
Solution Method
To enforce the zero inner perturbation potential condition, control points are placed just inside the configuration from each mesh vertex. To enforce the outer Neumann condition (either zero normal velocity or zero normal linearized mass flux), control points are placed on the outer surface of each panel at the centroid.
At trailing edges, multiple control points are placed in order to allow for the necessary break in velocity potential across the trailing edge. Care is taken to ensure these control points are distinct but still lie inside the surface.
Control points associated with superinclined base regions are automatically removed, and their associated source and doublet strengths are not included in the linear system of equations. This can be done because in supersonic flow disturbances only propagate downstream. If a superinclined base region is downstream of all other parts of the configuration being analyzed, then it may be treated as non-existent without any negative consequences. However, in order to ensure that the mesh is otherwise watertight, the user must mark all such superinclined surfaces as base regions.
The linear system of equations is assembled by looping through each control point and gathering the vector of influences from the surface source and doublet strengths on that control point. This vector then becomes one row of the AIC matrix. For internal control points, the potential influence of each panel is calculated. For external (centroid) control points, the velocity influence of each panel is calculated. The right-hand side of the linear system of equations is calculated based on the location of each control point, its associated surface normal vector, and the freestream velocity vector. The SLDS takes advantage of some knowledge of the structure of this linear system of equations to store the AIC matrix using minimal memory and also efficiently calculate matrix-vector products.
It should be noted that the AIC matrix and the right-hand vector are both heavily dependent upon the freestream direction and Mach number. Hence, any changes to these require that the linear system of equations be recalculated.
Once the linear system of equations has been assembled, it is solved using the generalized minimum residual (GMRES) algorithm. GMRES is an extremely efficient, iterative solver that successively improves estimates of based on the Cayley-Hamilton theorem. The implementation of GMRES is custom-implemented for FlightStream to allow for real-time updating the GUI as the solution progresses.
Post-Processing
One advantage to a Dirichlet-based formulation (where the inner perturbation potential is known) is that the surface velocity on each panel can be calculated exactly as a function of the panel source and doublet strengths. This makes calculating the surface velocity everywhere an operation. Since the inner perturation potential is zero, the velocity on the inner surface of each panel is simply the freestream velocity. The velocity on the outer surface is then just the freestream velocity plus the jump due to the source and doublet strengths
Once the surface velocity has been determined, the pressure coefficient may be determined from a several different pressure rules. The isentropic pressure rule is
The second-order pressure rule is
Applications of the SLDS
The supersonic linear-doublet solver is best suited for the analysis of slender configurations at low-supersonic Mach numbers (about ).
For modeling of inlets and outlets, it is not currently possible to apply inlet and outlet boundary conditions to closed faces. Instead, ducts and nacelles must be made flow-through. When doing so, it is imperative to have high mesh resolution on the interior of the duct so as to properly cancel out reflecting shock waves. A mesh that is not fine enough will result in erroneous pressure fluctuations on outside surfaces.
|
Note
|
Known Current Limitations
The development of the SLDS is ongoing. As such, certain aspects are still being improved, and the SLDS may not produce good results in certain instances. Some known instances are:
These limitations will be addressed in ongoing development. It is anticipated that future versions of FlightStream will include improvements to significantly enhance the accuracy and usability of the SLDS. |
Postprocessing
Loads Calculation
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Integer egestas
Drag Integration
FlightStream employs a dual approach for calculating drag:
-
Vorticity-Based Induced Drag Calculation: FlightStream offers a unique method for calculating induced drag that relies on user-defined trailing-edge boundary conditions. This method computes integrated circulation and downwash at the trailing edges to determine a downwash-based drag, conceptually similar to lifting line theory for arbitrary sectional load distributions. This feature, stemming from FlightStream’s vorticity-based formulation, offers a distinct perspective on induced drag estimation. Due to the closed-loop nature of the vorticity, this method is less mesh sensitive than the surface pressure integration method.
-
Surface Pressure Integration: This method leverages the Bernoulli equation to determine the pressure coefficient (Cp) at the surface of the body using the computed surface velocities. This method is applicable to all body types, including fuselages and bluff bodies. Only the pressure integration method is capable of capturing separation effects and off-body shocks. This integration lumps pressure and induced drag together.
The surface pressure integration method, explained in source, is based on applying Bernoulli’s equation to the body’s surface. The pressure coefficient (Cp) is calculated using the formula:
Nomenclature
English letter variables
| Variable | Description |
|---|---|
Skin friction coefficient for rough surfaces |
|
Auxiliary variable for turbulent boundary layer model |
|
Shape factor |
|
Compressible shape factor |
|
Shape factor: Difference between boundary layer thickness and displacement thickness |
|
Mach number at the edge of the boundary layer |
|
Reynolds number based on momentum thickness |
|
Reynolds number based on surface roughness height |
|
Surface of the immersed body |
|
Temperature at the edge of the boundary layer |
|
Recovery temperature |
|
Reference temperature |
|
Velocity at the outer edge of the boundary layer |
|
Normal blowing velocity |
|
Local velocity on the boundary |
|
Transformed coordinate in the phase plane |
|
Transformed coordinate in the phase plane |
|
Speed of sound at the edge of the boundary layer |
|
Skin friction coefficient |
|
Surface roughness height |
|
Unit normal vector |
|
Distance between two points in the flow field |
|
Coordinate along the local surface |
|
x-coordinate of the critical point |
|
y-coordinate of the critical point |
Greek letter variables
| Variable | Description |
|---|---|
Potential at point |
|
Average pressure gradient parameter |
|
Eigenvalue of the Jacobian matrix |
|
Doublet strength |
|
Eigenvalue of the Jacobian matrix |
|
Dynamic viscosity at recovery temperature |
|
Laplace operator |
|
Velocity field obtained from the potential function |
|
Potential flow function |
|
Potential flow function at a given interior point |
|
Freestream potential |
|
Source strength |
|
Momentum thickness |
|
Compressible momentum thickness |
|
Eigenvector components in the phase plane |
|
Coordinate along the surface streamline |
|
Eigenvector components in the phase plane |
|
Kinematic viscosity |
|
Boundary layer thickness |
|
Displacement thickness |
Appendix-A
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Integer egestas vulputate consequat. Proin libero mi, auctor sed orci nec, lobortis blandit massa. Nullam ut tellus eros. Nulla posuere diam in viverra imperdiet. Duis id ex facilisis, lacinia velit in, posuere nisl. In quis magna suscipit, tempus risus a, lacinia nulla. Morbi vulputate magna nisi, sed laoreet lectus scelerisque sed. Suspendisse bibendum dignissim erat, in egestas ipsum lobortis non. Praesent purus felis, porttitor et quam vel, consectetur ullamcorper quam. Etiam ut scelerisque massa. Duis maximus erat vel orci accumsan suscipit.
Glossary
Abbreviations
| Variable | Description |
|---|---|
UND |
University of North Dakota |
References
[1] N. H. Hoch, “Calculation of Aerodynamic Shape Sensitivities Using the Adjoint Method in a Subsonic/Supersonic Panel Code,” Master’s thesis, Utah University, Logan, Utah, 2024.
[2] W. M. Kutta, “Lift Forces in Fluid Flow,” Illustrierte Aeronautische Mitteilungen, p. 133, 1902.
[4] B. Stratford, “The Prediction of Separation of the Turbulent Boundary Layer,” Defense Technical Information Center, ADA091204, 1980. [Online]. Available: https://apps.dtic.mil/sti/tr/pdf/ADA091204.pdf.
[5] W. O. Valarezo and V. D. Chin, “A CPmax-Based Flow Separation Model for Application to Wings with High-Lift Devices,” Journal of Aircraft, vol. 31, no. 1, pp. 103–111, 1994, doi: 10.2514/3.46461.
[6] L. Morino, “Boundary Integral Equations in Aerodynamics,” Applied Mechanics Reviews, vol. 46, 1993.